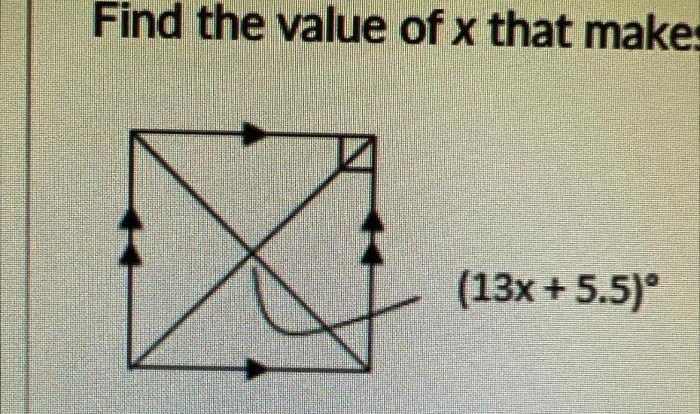
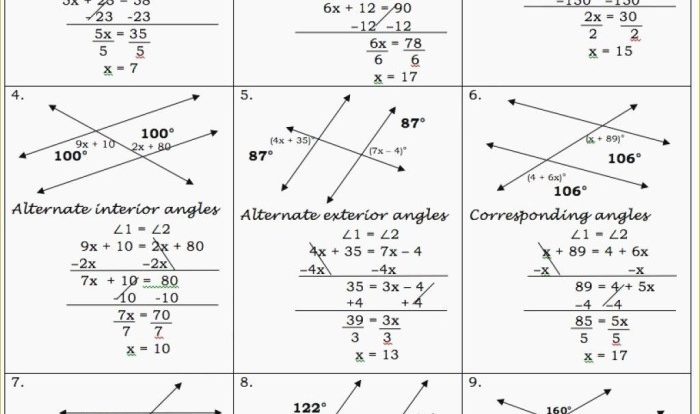
Embark on an educational journey with Lesson 3.2 Practice a Geometry Answers, a comprehensive guide that empowers you to grasp the intricacies of geometric concepts and hone your problem-solving abilities. Through a blend of theoretical explanations, practical examples, and detailed solutions, this resource equips you with the knowledge and skills necessary to excel in geometry and beyond.
This meticulously crafted guide delves into the fundamental principles of geometry, providing a solid foundation for understanding more complex concepts. Engage with interactive practice problems that reinforce your learning and develop your critical thinking abilities. Discover how geometric principles extend beyond the classroom, with real-world applications that demonstrate their relevance in various fields.
Lesson 3.2 Practice a Geometry

Geometri adalah cabang matematika yang berhubungan dengan bentuk, ukuran, dan posisi objek di ruang. Lesson 3.2 membahas konsep dan keterampilan dasar geometri, termasuk:* Titik, garis, bidang, dan ruang
- Sudut dan pengukuran sudut
- Segitiga dan sifat-sifatnya
- Segi empat dan sifat-sifatnya
- Lingkaran dan sifat-sifatnya
Konsep dan keterampilan ini sangat penting dalam berbagai bidang, termasuk arsitektur, teknik, dan seni. Misalnya, arsitek menggunakan geometri untuk merancang bangunan yang stabil dan estetis, sementara insinyur menggunakannya untuk membangun jembatan dan struktur lainnya yang aman dan efisien.
Practice Problems
- Tentukan jenis segitiga dengan panjang sisi 5 cm, 12 cm, dan 13 cm.
- Hitung luas persegi panjang dengan panjang 10 cm dan lebar 5 cm.
- Tentukan keliling lingkaran dengan jari-jari 7 cm.
Solusi:
1. Jenis segitiga
Segitiga siku-siku (karena 5^2 + 12^2 = 13^2)
2. Luas persegi panjang
10 cm x 5 cm = 50 cm^2
3. Keliling lingkaran
2πr = 2 x 3,14 x 7 cm = 43,96 cm
Applications
Konsep dan keterampilan geometri dapat diterapkan untuk memecahkan masalah di berbagai bidang matematika lainnya, termasuk:* Aljabar: Geometri dapat digunakan untuk memvisualisasikan dan menyelesaikan persamaan dan pertidaksamaan.
Kalkulus
Geometri digunakan untuk menghitung luas, volume, dan panjang kurva.
Statistik
Geometri digunakan untuk merepresentasikan dan menganalisis data.Selain itu, konsep dan keterampilan geometri juga digunakan dalam berbagai bidang praktis, seperti:* Navigasi: Geometri digunakan untuk menentukan lokasi dan arah.
Seni dan desain
Geometri digunakan untuk menciptakan karya seni dan desain yang seimbang dan estetis.
Arsitektur
Geometri digunakan untuk merancang bangunan yang fungsional dan menarik.
Assessment, Lesson 3.2 practice a geometry answers
Tabel Konsep dan Keterampilan| Konsep/Keterampilan | Deskripsi ||—|—|| Titik, garis, bidang, dan ruang | Konsep dasar geometri || Sudut dan pengukuran sudut | Mengukur dan mengklasifikasikan sudut || Segitiga dan sifat-sifatnya | Sifat-sifat segitiga yang berbeda || Segi empat dan sifat-sifatnya | Sifat-sifat segi empat yang berbeda || Lingkaran dan sifat-sifatnya | Sifat-sifat lingkaran yang berbeda |Self-Assessment Checklist* Saya dapat mengidentifikasi titik, garis, bidang, dan ruang.
- Saya dapat mengukur dan mengklasifikasikan sudut.
- Saya dapat menentukan sifat-sifat segitiga.
- Saya dapat menentukan sifat-sifat segi empat.
- Saya dapat menentukan sifat-sifat lingkaran.
Praktik Tambahan* Selesaikan soal latihan di akhir Lesson 3.2.
- Buatlah model segitiga, segi empat, dan lingkaran menggunakan bahan-bahan seperti kardus atau tanah liat.
- Gunakan aplikasi geometri untuk menjelajahi konsep dan keterampilan geometri.
Key Questions Answered: Lesson 3.2 Practice A Geometry Answers
What are the key concepts covered in Lesson 3.2?
Lesson 3.2 covers fundamental geometric concepts such as angles, triangles, quadrilaterals, circles, and transformations.
How can I apply the skills learned in Lesson 3.2 to other areas of mathematics?
The concepts and skills learned in Lesson 3.2 provide a foundation for understanding more advanced topics in mathematics, such as trigonometry, calculus, and statistics.
Where can I find additional practice problems to reinforce my understanding?
This guide provides a comprehensive set of practice problems. Additional problems can be found in textbooks, online resources, and workbooks.